問：哪種方案最好?

　　繪制該問題的決策樹，如圖1一9所示。

　　方案l(結點①)的期望收益為：[0.7×100 0.3×(一20)]×10—300=340(萬元)

　　方案2(結點②)的期望收益為：(0.7×40 0.3×30)×10一140=230(萬元)

　　至于方案3，由于結點④的期望收益465(=95×7—200)萬元大于結點⑤的期望收益280(=40×7)萬元，所以銷路好時，擴建比不擴建好。方案3(結點③)的期望收益為：(0.7×40×3 0.7×465 0.3×30×10)一140=359.5(萬元)

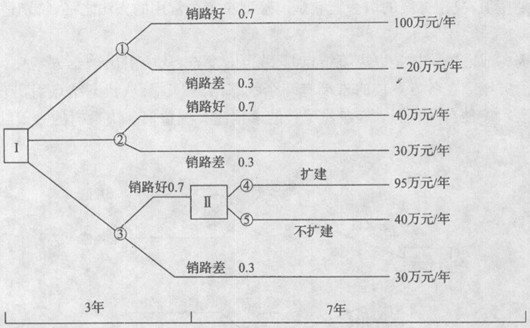
　　圖1—9 決策樹

　　計算結果表明，在三種方案中，方案3最好。

　　需要說明的是，在上面的計算過程中，我們沒有考慮貨幣的時間價值，這是為了使問題簡化。但在實際中，多階段決策通常要考慮貨幣的時間價值。

　　3.不確定型決策方法 。

　　不確定型決策是指在決策所面臨的自然狀態(tài)難以確定而且各種自然狀態(tài)發(fā)生的概率也無法預測的條件下所做出的決策。由于自然狀態(tài)下決策結果的不可知，因此具有極大的風險性和主觀隨意性。不確定型決策常遵循以下幾種思考原則。

　　(1)樂觀原則。樂觀原則是指愿承擔風險的決策者在方案取舍時以各方案在各種狀態(tài)下的最大損益值為標準(即假定各方案最有利的狀態(tài)發(fā)生)，在各方案的最大損益值中取最大者對應的方案。

　　【例6】 某企業(yè)擬開發(fā)新產(chǎn)品，有三種設計方案可供選擇。因不同的設計方案的制造成本、產(chǎn)品性能各不相同，在不同的市場狀態(tài)下的損益值也各異。有關資料如表l—4所示：

　　表1—4 數(shù)據(jù)表

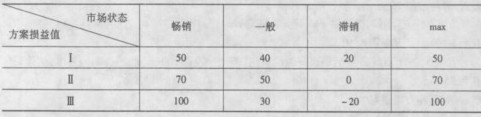
　　在不知道各種狀態(tài)的概率時，用樂觀原則選擇方案的過程如下：

　　①在各方案的損益中找出最大者；

　　②在所有方案的最大損益值中找最大者，即max{50，70，100}=100，它所對應的方案Ⅲ就

　　是用該原則選出的方案。

　　(2)悲觀原則。悲觀原則是指決策者在進行方案取舍時以每個方案在各種狀態(tài)下的最小值為標準(即假定每個方案最不利的狀態(tài)發(fā)生)，再從各方案的最小值中取最大者對應的方案。

　　仍以上表資料為例，用悲觀原則決策時先找出各方案在各種狀態(tài)下的最小值，即{20，0，-20}，然后再從中選取最大值：max{20，0，-20}=20，對應的方案I即為用悲觀原則選取的決策方案。該方案能保證在最壞情況下獲得不低于20單位的收益，而其他方案則無此保證。

　　(3)折中原則。悲觀原則和樂觀原則都是以各方案不同狀態(tài)下的最大或最小極端值為標準的。但多數(shù)情況下決策者既非完全的保守者，亦非極端冒險者，而是在介于兩個極端的某一位置尋找決策方案，即折中原則。折中原則的決策步驟如下：